Diese Seite funktioniert nur mit Javascript.
Mathematische Herleitung der Transformationskurve5.1.3 Tausch und ProduktionDie Normative Theorie
isher haben wir getrennt voneinander untersucht, wie eine Volkswirtschaft vorgegebene Gütermengen effizient verteilen und wie sie mit vorgegebenen Faktormengen diese Güter effizient produzieren kann. Nun liegt es natürlich nahe, diese beiden Prozesse miteinander zu verbinden und der Frage nachzugehen, wie das Allokationsproblem bei gegebenen Präferenzen und gegebener Faktorausstattung effizient gelöst werden kann.
Dabei bleiben die Gleichgewichtsbedingungen der beiden vorangegangenen Abschnitte natürlich unverändert gültig, da - egal welche Produktion sich in irgendeiner Weise als optimal erweist - sie im Anschluss nicht ineffizient verteilt werden darf und ineffiziente Produktion - also die Verschwendung von Produktionsfaktoren - von vornherein sinnlos ist. M.a.W., für eine effiziente Lösung des Gesamtproblems ist die effiziente Lösung aller Teilprobleme erforderlich. Im Tauschbereich müssen als die Grenzraten der Substitution über alle Konsumenten gleich sein und im Produktionsbereich die Grenzraten der technischen Substitution in allen Unternehmen.
Im Folgenden betrachten wir den Produktionssektor der Volkswirtschaft als rein technischen Bereich, in dem keinem Individuum irgendein Nutzen oder Disnutzen zuteil wird. Es erfordert insbesondere nicht die Annahme gewinnmaximierender Unternehmer, um die dritte Bedingung (und damit die letzte) für ein Allgemeines Gleichgewicht abzuleiten. Der Einfachheit halber sprechen wir wieder von einer eigeninteressenlosen übergeordneten Instanz, die allein die Nutzen der beiden Konsumenten im Auge hat, ohne diese in irgendeiner Weise zu gewichten. Die Aufgabe dieser Instanz soll es sein, bei einer gegebenen Ausgangsverteilung der Güter (in unserem Beispiel von Zigaretten und Bier) über die Konsumenten zu überprüfen, ob durch eine andere Allokation der Produktionsfaktoren eine Verbesserung der Situation im Sinne des Pareto-Kriteriums erreicht werden kann. Wie wir sogleich sehen werden, ist diese Aufgabe überraschend einfach lösbar.
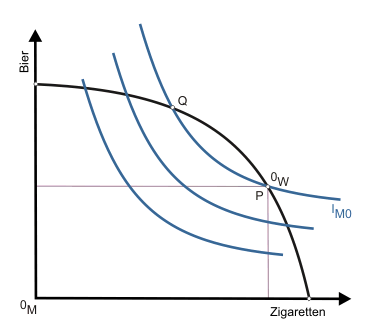
Dazu geben wir die in Abbildung 1 wiedergegebene Situation vor. Auf der Transformationskurve, d.h. die Bedingung technischer Effizienz ist erfüllt, wird im Punkt P produziert. Da Bier- und Zigarettenmenge damit bestimmt sind, kann der Punkt P als oberer rechter Punkt für eine Edgeworth-Box benutzt werden. Er soll Ursprungspunkt für ein Indifferenzkurvenschema der Konsumentin sein. Der eigentliche Ursprung ist Ursprungspunkt für ein Indiffferenzkurvenschema des Konsumenten. Die Höhe der Box zeigt die gesamte Bier-, die Länge die Zigarettenproduktion.
Es sind lediglich Indifferenzkurven für den Konsumenten dargestellt, da wir zunächst von dem Spezialfall ausgehen wollen, dass der Konsument alle, die Konsumentin keine Güter erhält. Etwas ungewöhnlich mag erscheinen, dass die Indifferenzkurven des Konsumenten über die Ränder der Edgeworth-Box hinausgehen. Dies ist jedoch korrekt, denn schließlich ist eine der getroffenen Annahmen Vollständigkeit der Präferenzen (allein aus ästhetischen Gründen werden die Indifferenzkurven in den meisten grafischen Darstellungen der Box an deren Rändern abgeschnitten).
Da auf der Transformationskurve produziert wird, muss die Instanz der Frage technischer Effizienz nicht weiter nachgehen. Auch im Tauschbereich allein kann durch eine Umverteilung von Gütern keine Situationsverbesserung im Sinne des Pareto-Kriteriums erzielt werden, denn da die Konsumentin im Punkt P über keine Güter verfügt, kann der Konsument bei jeder anderen denkbaren Güterverteilung nur schlechter dastehen.
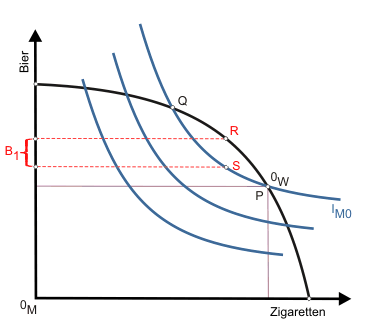
Der Instanz bleibt also nur zu untersuchen, ob durch eine Umstrukturierung der Produktion eine paretianische Verbesserung der Situation herbeigeführt werden kann. Dies ist offensichtlich der Fall, da eine Produktion zwischen P und Q mehr Güter bereitstellt als notwendig sind, um den Konsumenten auf seinem durch die Indifferenzkurve IM0 angezeigten Nutzenniveau zu halten. Unabhängig von der Verteilung der überschüssigen Gütermengen zwischen Konsument und Konsumentin wird immer eine Verbesserung im Sinne des Pareto-Kriteriums erreicht.
Alternativ macht man sich die Ineffizienz des Punktes P mit folgender Überlegung klar: Wandert der Konsumnet auf der Indifferenzkurve nach oben, dann befindet sich die Produktion unterhalb der Transformationskurve. Diese Punkte sind aber erreichbar, ohne dass die Produktionsfaktoren vollbeschäftigt wären. Das aktuelle Nutzenniveau des Konsumenten ließe sich also bei Unterbeschäftigung realisieren.
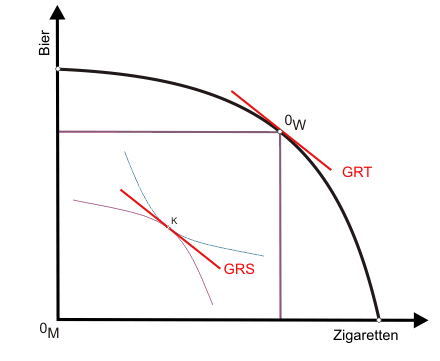
Dass eine Verbesserung der Ausgangssituation möglich ist, lässt sich offenbar auf die von Indifferenzkurve und Transformationskurve gebildete Linse mit den Ecken Q und P zurückführen. Ursache dieser Linse ist das Auseinanderfallen von Grenzrate der Substitution (Tausch, Steigung der Indifferenzkurve) und Grenzrate der Transformation (Produktion, Steigung der Transformationskurve) im Punkt P. Daraus folgt im Umkehrschluss:
Diese dritte Bedingung für ein Allgemeines Gleichgewicht gilt nicht nur für den hier unterstellten Spezialfall, dass einer der beiden Konsumenten ausgangs alle Güter erhält. Auch sonst muss die Grenzrate der Transformation der Grenzrate der Substitution entsprechen. Die alleinige Orientierung an den Nutzen der Individuen ist der Grund. In ihrer im Tausch oder sonstwie herausgebildeten übereinstimmenden Grenzrate der Substitution kommt eine Bewertung der Güter zum Ausdruck, der vom rein technisch gesehenen Produktionsapparat Rechnung getragen werden muss. Wenn beide Konsumenten ein Bier mit zwei Schachteln Zigaretten bewerten und ihr Urteil allein maßgeblich sein soll, dann müssen auch in der Produktion die Alternativkosten eines Bieres zwei Schachteln Zigaretten entsprechen. Würden sie hingegen nur einer Schachtel entsprechen, müsste die Bierproduktion auf Kosten der Zigarettenproduktion ausgedehnt werden (durch vollständige Spezialisierung kommt es evtl. zu einer Randlösung). Dann nämlich würde ein von den Konsumenten mit zwei Zigarettenschachteln bewertetes Bier kostendeckend durch Aufgabe nur einer Schachtel produziert. Mit der zweiten Schachtel "erhöht die Instanz die Wohlfahrt", wie auch immer sie deren Inhalt unter den Konsumenten verteilt.
Zusammengefasst lauten also die drei Bedingungen für ein Allgemeines Gleichgewicht:
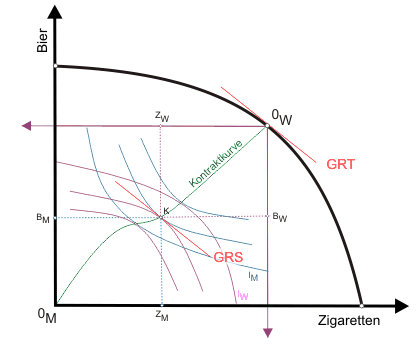
Abbildung 2 zeigt ein Allgemeines Gleichgewicht.
Wie viele Allgemeine Gleichgewichte, also Situationen auf die alle drei genannten Bedingungen zutreffen, gibt es nun? Die Antwort ist: unter unseren Bedingungen evtl. keines, aber es sind auch unendlich viele möglich. Keines gibt es zum Beispiel in dem Fall, dass beide Konsumenten sich aus einem der beiden Güter gar nichts machen. Nehmen wir an, beide erfahren nur Nutzen aus dem Konsum von Zigaretten und keinen Nutzen aus dem Konsum von Bier. Die Indifferenzkurven in der in Abbildung 2 eingezeichneten Edgeworth-Box verliefen dann für beide Konsumenten senkrecht. Eine Kontraktkurve wäre nicht mehr auszumachen. In jedem Punkt in der Box wäre die Gleichgewichtsbedingung im Tauschbereich erfüllt. Die Gerade, die die Grenzrate der Substitution anzeigt, verliefe senkrecht. Eine entsprechende Grenzrate der Transformation muss es aber nicht geben (das ist abhängig von der Technologie). Es käme zu einer Randlösung im Endpunkt der Transformationskurve auf der Abszisse.
Die Möglichkeit unendlich vieler Allgemeiner Gleichgewichte macht man sich (wieder einmal) am einfachsten an einem Spezialfall klar. Nehmen wir an, beide Konsumenten besäßen die gleiche Nutzenfunktion. Die Diagonale in der Edgeworth-Box wäre dann die Kontraktkurve. Sind die Nutzenfunktionen zusätzlich homogen, dann ist die Grenzrate der Substitution auf der diagonalen Kontraktkurve konstant (bei homogenen Nutzenfunktionen ist der Grenznutzen nur von der Güterintensität, nicht aber vom Konsumniveau abhängig). Findet sich auf der Transformationskurve eine entsprechende Grenzrate der Transformation, so existieren allein für diesen einzigen Produktionspunkt unendlich viele Allgemeine Gleichgewichte (zwar unterscheiden sich diese durch die Verteilung der Güter, sprich: der Einkommen, zwischen den Konsumenten, was jedoch für die drei Bedingungen unerheblich ist). Sie können jedoch auch bei unterschiedlichen Präferenzen zustande kommen, da sich unter der Transformationskurve unendlich viele Edgeworth-Boxen konstruieren lassen. Für jede dieser Boxen ist dann theoretisch eine Grenzrate der Substitution auf der Kontraktkurve denkbar, die mit der entsprechenden Grenzrate der Transformation übereinstimmt. Zu jedem dieser Gleichgewichte gehört allerdings eine andere Verteilung der Ressourcen (Vermögen, Produktionsmittel) zwischen den Wirtschaftssubjekten. Mit einer gegebenen Vermögensverteilung wäre das Gleichgewicht eindeutig determiniert.
Auf eine mathematische Ableitung der dritten Gleichgewichtsbedingung wird an dieser Stelle verzichtet, da zum Abschluss des Kapitels "Die Normative Theorie" eine mathematische Herleitung der Bedingungen für ein Wohlfahrtsmaximum erfolgt, in denen neben einer weiteren alle drei notwendigen Bedingungen des Allgemeinen Gleichgewichts enthalten sind.